Joint work with Charles Bouveyron and Julie Delon — full text available on HAL
NEW: python demo available HERE
Abstract: This work addresses the problem of patch-based image denoising through the unsupervised learning of a probabilistic high-dimensional mixture models on the noisy patches. The model, named hereafter HDMI, proposes a full modeling of the process that is supposed to have generated the noisy patches. To overcome the potential estimation problems due to the high dimension of the patches, the HDMI model adopts a parsimonious modeling which assumes that the data live in group-specific subspaces of low dimensionalities. This parsimonious modeling allows in turn to get a numerically stable computation of the conditional expectation of the image which is applied for denoising. The use of such a model also permits to rely on model selection tools, such as BIC, to automatically determine the intrinsic dimensions of the subspaces and the variance of the noise. This yields a blind denoising algorithm that demonstrates state-of-the-art performance, both when the noise level is known and unknown.
context: Patch-based image denoising with Bayesian framework
The classical denoising model can be expressed in the patch space under the form:
Y = X + N
where X is the unknown patch before degradation and Y is the observed patch, degraded by some additive noise N. The noise N is assumed Gaussian and white.
The Bayesian framework: the vector X is assumed to follow a given distribution p(x; θ) with parameters θ. This gives a natural estimator for X with the Minimum Mean Square Error estimator (MMSE) x = E(X|Y= y).
In general, the distribution p(x; θ) is chosen to be Gaussian or a Mixture of Gaussian.
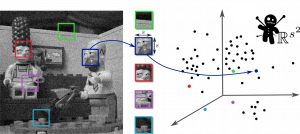
The curse of dimensionality
In order to take advantage of the self-similarity of the images, the patches should be large enough (typically 5×5 pixels to 10x10pixels). Thus the patch-space has a dimensionality of ~100 which is considered a high-dimensional space !

This implies numerical issues for the inference of the parameters θ of the prior distribution!
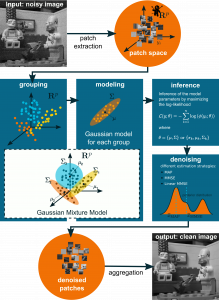
HDMI: a model that take advantage of the high-dimensionality of the patch-space


Results and experiments
An example of HDMI denoising:
Noisy image |
Clustering from HDMI |
Denoised with HDMI |
The regularization effect of the dimension reduction :

quite fuzzy and the denoising result (middle) is not very good (PSNR: 28.92dB). Second line: Denoising with the HDMI model (50 groups) with intrinsic dimension regularization during the EM process. The clustering (left) is smoother and the denoising yields better results (PSNR: 29.28dB). The noise variance is σ = 30 and a zoom on the denoising results is proposed in the left column.
More results are presented hereafter:
| Flower | Traffic | |
| Noisy |  |
 |
| NL-bayes |  |
 |
| BM3D |  |
 |
| S-PLE |  |
 |
| HDMI |  |
 |
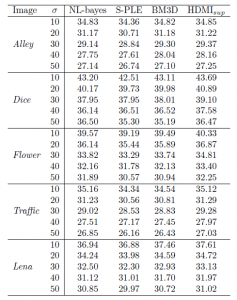
PSNR table: Comparison of HDMI, NLBayes, SURE-PLE and BM3D for color images. The HDMI algorithm is performed with K = 50 and the NL-Bayes, SURE-PLE and BM3D algorithms are run from www.ipol.im with default settings. The PSNRs are averaged on five noise realization and rounded at precision 10e-2.
Going further: other image inverse problems
Recover pixel missing at random: the EM algorithm is well designed for this kind of problem!
corrupted image: